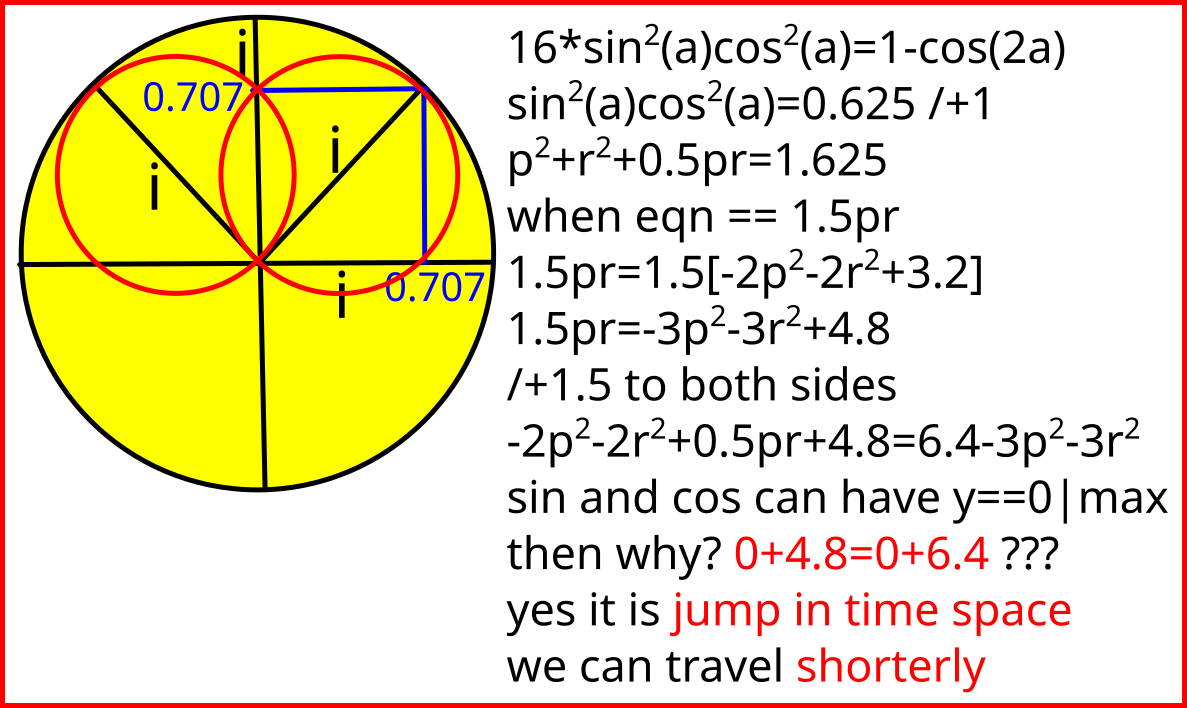
 Interesting: r^3-z^3=x^2+y^2=x+y+z where x^2+y^2=x+y+1; x(x-1)=y(1-y)+1 where -x/y=(1-y)/(x-1)+2x/x-y/y and (y-x)/y=(1-y)/(x-1)+2 and (y-x)/y-1=(y-1)/(1-x)+1 proving [x,y]=[1,1] for -1==1 and which function is y=x for -1=--1 so i^2=-i^2 yes a line on complex plane, in both ends connected line via infinity is again a half loop 🙂 The upper drawn question uprises for us ^^^ See my computation.
Interesting: r^3-z^3=x^2+y^2=x+y+z where x^2+y^2=x+y+1; x(x-1)=y(1-y)+1 where -x/y=(1-y)/(x-1)+2x/x-y/y and (y-x)/y=(1-y)/(x-1)+2 and (y-x)/y-1=(y-1)/(1-x)+1 proving [x,y]=[1,1] for -1==1 and which function is y=x for -1=--1 so i^2=-i^2 yes a line on complex plane, in both ends connected line via infinity is again a half loop 🙂 The upper drawn question uprises for us ^^^ See my computation.

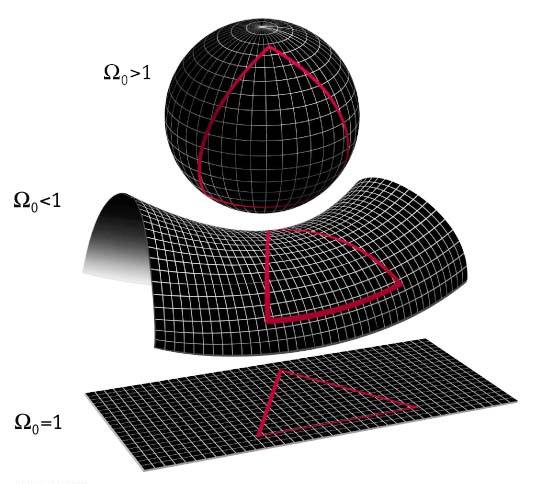
Do 3 types of space define worm hole shortcut? Computation:
Comments “Do 3 types of space define worm hole shortcut? Computation:”